Area of a circle

Area A = π x r²

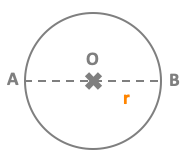
with π (number pi) approximately equal to 3.14
Radius = AO = OB = r
Diameter = AB = 2 r

Example

Take a circle with radius r = 3 cm
Area A of the circle = π x r² ≈ 3.14 x 3² ≈ 28.26 cm²

Calculate the area of a circle

Circle

The circle is a fundamental geometric shape that has been studied and admired for centuries. A circle is a two-dimensional geometric shape characterized by all points in a plane that are equidistant from a fixed point called the center. The distance from the center to any point on the circle is known as the radius.

The center of the circle is the fixed point in the middle of the circle. The radius of the circle is the distance from the center to any point on the circle. All radii of a circle are of equal length. Furthermore, the diameter of a circle is a straight line passing through the center of the circle and touching two points on the circumference. The diameter is twice the length of the radius. The circumference of a circle is the perimeter or boundary of the circle.

The formula to calculate the area (A) of a circle is given by A = π r ² where where: A is the area of the circle, π (pi) is a mathematical constant approximately equal to 3.14159 and r is the radius of the circle.
To use this formula, you need to know the value of the radius. If you are given the diameter (d) instead of the radius, you can use the relationship r = d / 2 to find the radius and then substitute it into the formula.

The concept of the circle and its study dates back to ancient civilizations.

Properties of the circle

Circles are symmetrical. Indeed any line passing through the center divides the circle into two equal halves.
All radii of a circle are congruent (have the same length).
Tangent to a circle at any point is perpendicular to the radius at that point.
The radius (r) of a circle is the distance from the center to any point on the circle.
The diameter (d) is the distance across the circle through its center and is twice the length of the radius (d = 2 r).
A chord is a line segment that connects two points on the circle. The diameter is a special chord that passes through the center.
A tangent is a line that touches the circle at exactly one point, known as the point of tangency. The radius at the point of tangency is perpendicular to the tangent.
A circle is symmetric with respect to any line passing through its center.

Examples

Example 1:

Suppose you have a circle with a radius of 6 centimeters. Calculate the area of the circle.
A = π r²
A = π × 6² = 36 π square centimeters
Using an approximate value for π (let's use 3.14), you can find the numerical approximation:
A ≈ 36 × 3.14 ≈ 113.04 square centimeters
So, the area of the circle is approximately 113.04 square centimeters.

Example 2:

If you have a circle with a diameter of 10 meters, first find the radius (r = d / 2) and then calculate the area.
r = 10 / 2 = 5 meters
A = π × 5² = 25 π square meters
Using an approximate value for π (3.14), you can find the numerical approximation:
A ≈ 25 × 3.14 ≈ 78.5 square meters
So, the area of the circle is approximately 78.5 square meters.

Example 3:

Consider a circle with a radius of 8 inches. Calculate its area.
A = π × 8² = 64 π square inches
Using an approximate value for π, you can find the numerical approximation:
A ≈ 64 × 3.14 ≈ 200.96 square inches
So, the area of the circle is approximately 200.96 square inches.