Area of a trapezium |
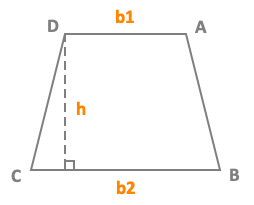
|
|
(b1 + b2) x h
2
|
|
DA = base 1 = b1 CB = base 2 = b2 h = height ExampleABCD is a trapezoid with a base b1 = 2 cm, a base b2 = 7 cm and a height h = 4 cmArea A of a trapezoid ABCD =
(b1 + b2) x h
2
=
(2 + 7) x 4
2
=
9 x 4
2
= 18 cm²
Calculate the area of a trapezium |
TrapeziumA trapezium is a quadrilateral with at least one pair of parallel sides. The parallel sides are called bases, and the non-parallel sides are legs. The height, or perpendicular distance between the bases, is crucial for calculating the area. The formula for the area of a trapezium is A = (b1 + b2) * h / 2, where A is the area, b1 and b2 are the lengths of the bases, and h is the height.A trapezium is a quadrilateral with at least one pair of parallel sides; it can be isosceles or scalene. The mid-segment, parallel to the bases, equals their average length. Properties include a sum of interior angles totaling 360 degrees, intersecting diagonals, and supplementary angles at the bases. The angle bisectors of the non-parallel sides are concurrent. The line segment connecting the midpoints of the non-parallel sides is parallel and equal to half the sum of the bases. A trapezium can be inscribed in a circle if and only if it is an isosceles trapezium. Consecutive angles in a trapezium are supplementary. The area of a trapezium can also be expressed as the product of its height and the average of the lengths of its bases. There are two main types of trapeziums based on the lengths of their sides. In an isosceles trapezium, one pair of opposite sides (bases) are of equal length, and the non-parallel sides (legs) may have different lengths. A scalene trapezium is one in which all four sides have different lengths. Both pairs of opposite sides are of unequal length. Furthermore, a right trapezium typically refers to a trapezium or trapezoid where one of the angles formed by a non-parallel side and a base is a right angle (90 degrees). In other words, a right trapezium is a trapezium that has one right angle among its four interior angles. To visualize, if you have a trapezium and draw an altitude from one of the non-parallel sides to the base, the angle formed at the point where the altitude meets the base would be a right angle. The other three angles in the trapezium could be acute or obtuse, but one of them is guaranteed to be a right angle. In India, the term "trapezium" is commonly used to describe a quadrilateral with no parallel sides. The term "trapezoid" is not as commonly used in Indian mathematics education. The preference for the term "trapezium" aligns more with the British convention. ExamplesHere are two examples of how to calculate the area of a trapezium:Example 1:Consider a trapezium with bases b1 = 8 units and b2 = 12 units, and a height h = 5 units.The area of the trapezium A = (b1 + b2) / 2 x h = (8 + 12) / 2 × 5 = 10 × 5 = 50 square units So, the area of the trapezium is 50 square units. Example 2:Let's take another trapezium with bases b1 = 15 cm2, b2 = 9 cm2 and a height h = 8 cm2.A = (b1 + b2) / 2 x h = (15 + 9) / 2 × 8 = 12 × 8 = 96 cm2 Thus, the area of this trapezium is 96 square centimeters. |