Area of a parallelogram

Area A = b x h

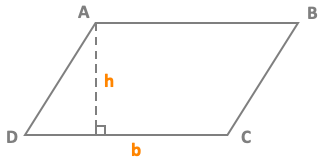
DC = base = b
h = height

Example

ABC is a parallelogram with a base b = 8 cm and a height h = 2 cm
Area A of a parallelogram ABCD = b x h = 8 x 2 = 16 cm²

Calculate the area of a parallelogram

Parallelogram

A parallelogram is a quadrilateral with opposite sides parallel. Its opposite angles are equal, and consecutive angles are supplementary. The diagonals bisect each other, creating two congruent triangles. The area is found by multiplying base length and height.

Parallelograms exhibit symmetry, where opposite sides and angles are equal. The opposite sides also have equal length. The sum of interior angles is always 360 degrees. Parallelograms include rectangles, rhombi, and squares, each with unique properties. The opposite angles of a parallelogram are supplementary, meaning they add up to 180 degrees. The area of a parallelogram can also be expressed as the magnitude of the cross product of its adjacent sides' vectors.

Hera are some properties of a parallelogram. Opposite sides of a parallelogram are parallel. Opposite angles are equal. Consecutive angles are supplementary (add up to 180 degrees). Opposite sides are equal in length. Opposite angles are equal in measure. Diagonals bisect each other, meaning they intersect at their midpoints. Consecutive angles are supplementary, meaning the sum of two consecutive angles is 180 degrees. Parallelograms are symmetric about their midpoints. Special cases of parallelograms have additional properties. For example, a rectangle has right angles, a rhombus has all sides equal, and a square is both a rectangle and a rhombus.

Below you will find special cases of parallelograms.

Rectangle

A rectangle is a parallelogram with all angles equal to 90 degrees (right angles). Opposite sides are parallel and equal in length.

Rhombus

A rhombus is a parallelogram with all sides equal in length. Opposite angles are equal, but they are not necessarily right angles.

Square

A square is a special type of rectangle and rhombus. It has all sides equal and all angles equal to 90 degrees. Opposite sides are parallel, and diagonals bisect each other at right angles.

Examples

We will find below 2 examples of calculating the area of a parallelogram.

Example 1:

Consider a parallelogram with base b = 10 units and height h = 6 units.
A = b x h = 10 x 6 = 60 square units
Thus, the area of the parallelogram is 60 square units.

Example 2:

Take another parallelogram with base b = 12 cm² and height h = 8 cm².
A = b x h = 12 x 8 = 96 cm²
So, the area of this parallelogram is 96 square centimeters.