Area of a rhombus

Area A =

d1 x d2 / 2

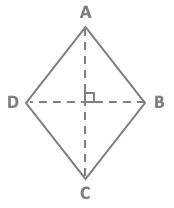
Diagonal 1 = d1
Diagonal 2 = d2
AB = BC = CD = DA

Example

Take a rhombus with diagonal 1 d1 = 6 cm and diagonal 2 d2 = 2 cm.
Area A of the rhombus =

d1 x d2 / 2

6 x 2 / 2

= 6 cm²

Calculate the area of a rhombus

Rhombus

A rhombus is a quadrilateral (four-sided polygon) with all sides of equal length. Its opposite angles are equal, and the diagonals bisect each other at right angles. The area of a rhombus is given by the formula: Area = (diagonal1 * diagonal2) / 2 or by base times height. Rhombi often appear in various fields, including geometry, where their properties are studied, and in design, where their symmetrical and balanced shape is appreciated. In colloquial language, people may refer to a rhombus as a "diamond," particularly when discussing shapes in jewelry or patterns like playing cards.

A rhombus is a special type of parallelogram with unique properties. Its diagonals not only bisect each other but also form four congruent right-angled triangles. The sum of opposite angles is always 180 degrees. Rhombi are prevalent in fields like mathematics, engineering, and design due to their symmetry and versatility. In nature, crystals and certain molecules exhibit rhombic shapes. Understanding the properties of a rhombus contributes to solving geometric problems and has practical applications in diverse areas of science and art.

Properties of a rhombus

You can find below some key properties of a rhombus:

Equal side lengths:

All four sides of a rhombus are of equal length.

Opposite angles:

Opposite angles in a rhombus are equal.

Diagonals bisect angles:

The diagonals of a rhombus bisect the angles at the vertices.

Diagonals perpendicular:

The diagonals of a rhombus are perpendicular to each other.

Diagonals bisect each other:

The diagonals of a rhombus bisect each other at right angles, forming four congruent right-angled triangles.

Consecutive angles supplementary:

The sum of consecutive angles in a rhombus is always 180 degrees.

Rhombus is a parallelogram:

A rhombus is a type of parallelogram, which means it has opposite sides that are parallel.

Symmetry:

A rhombus exhibits symmetry through its diagonals, dividing it into two congruent mirror-image halves.

Diagonals equal length:

In a rhombus, the two diagonals are of equal length.

Examples

Let's consider two examples of calculating the area of a rhombus:

Example 1:

Suppose you have a rhombus with diagonals of length 8 cm and 10 cm.
Area = (diagonal1 * diagonal2) / 2
Area = (8 cm * 10 cm) / 2
Area = 40 cm²

Example 2:

Imagine a rhombus with diagonals measuring 12 meters and 16 meters. Area = (diagonal1 * diagonal2) / 2 Area = (12 m * 16 m) / 2 Area = 96 m²

These examples illustrate how to apply the area formula for a rhombus, which involves multiplying the lengths of the diagonals and dividing the result by 2.